ARM Assembly Base64 Encoder: Part 1
In this three part series, I will first go over Base64 Encoding, then in Part 2, talk about ARM Assembly and finally in part 3, code up a Base64 encoder.
Table of Contents
Back in school, we used a program called ARMSim# to learn ARM assembly with the ARM7TDMI instruction set. That software runs on Windows and includes both, an assembler and a linker.
Lately, I wanted to refresh my ARM knowledge, but this time I wanted to code ARM directly on ARM based hardware. You could possibly emulate a home router with QEMU but setting that up is a bit more complex. Previously for practice, I did have a root shell on a home router that was manufactured by a company I used to work for, which used the ARM7L CPU. Since home routers are somewhat locked from factory, getting a root shell is pretty much non-existent without some vulnerability that would give you that remote shell access. So, since Raspberry Pi’s are much more accessible and easier to work with, a Raspberry Pi will have to do. I will be using a Raspberry Pi 3 which technically has a 64-bit ARM8 CPU but ARM is backwards compatible and can run in 32-bit mode.
The Base64 Encoding Process
Before we start coding up the Base64 encoder in ARM, we have to understand the process on how Base64 gets encoded from a string. Let’s convert the string Hel. Once we understand the process, we will convert the entire string Hello World.
The first step is to break the binary string down into 6-bit blocks. Why? Because Base64 maps every three bytes of data into four bytes of encoded data. To make this evenly divisible by those 4 bytes, we can put together 24 bits (three bytes is 3*8=24 bits). This will make sense later. For now, H on the ASCII table is the 73rd item, with an index/decimal value of 72 and it’s hexadecimal value of 48. In binary, that is 01001000, converted from it’s decimal value. Remember, in binary, starting from right to left we have 2 to the n’th power: 2^0=1, 2^1=2, 2^2=4, 2^3=8, 2^4=16, 2^5=32, 2^6=64… and so on. For every value that’s a 1, we add it. So, 01001000 is 2^3 = 8 + 2^6 = 64 which equals 72.
Lowercase e is 101 in decimal and lowercase l is 108 in decimal. Converting those to binary, we get 01100101 and 01101100 respectively.
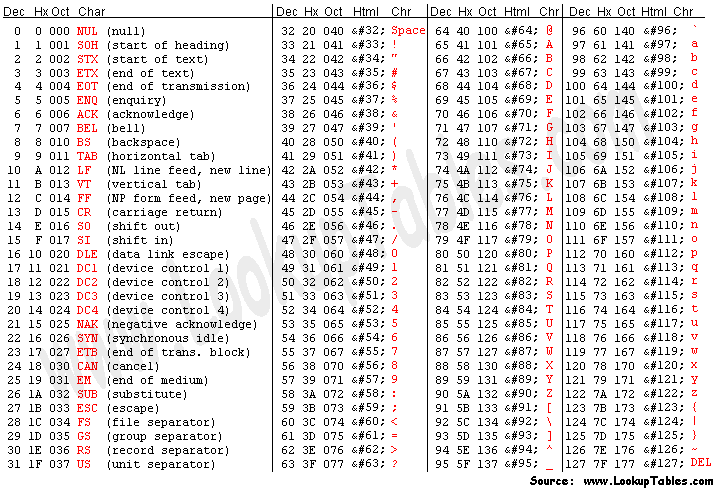ASCII Table
Remember I said that Base64 converts every three bytes of data? We have 3 exact bytes (24 bits). Lets put them together. In binary you end up with:
String: H e l
Decimal: 72 101 108
Binary: 01001000 01100101 01101100
Result: 010010000110010101101100
Now that we have 24 bits, Base64 encoding will divide the binary data up to six-bit chunks and map them to a base64 character according to the table Base64 table which we will look at in just a moment. For now lets separate the 24-bits into those 6-bit chunks.
010010000110010101101100
will separate to:
010010 | 000110 | 010101 | 101100
Let’s look at the Base64 table.
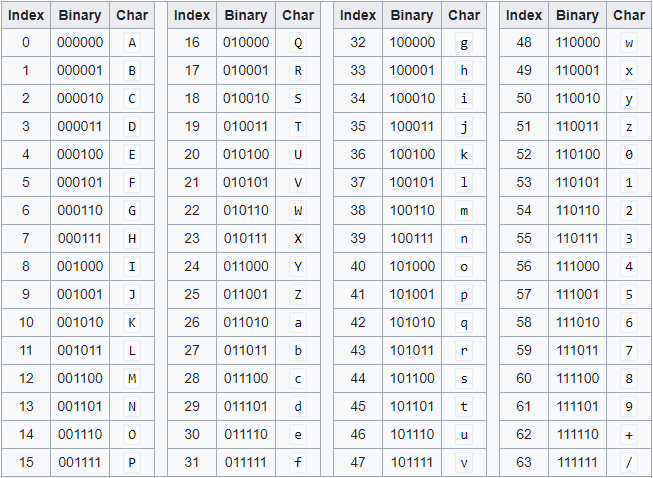Base64 Table
The 64 characters (hence the name Base64) are 26 uppercase characters, 26 lowercase characters, 10 digits, then the Plus sign (+) and the Forward Slash (/), in that order. There is also a 65th character known as a pad, which is the Equal sign (=). This character is used when the last segment of binary data doesn’t contain a full 6 bits. This padding is VERY important and will make sense once we convert data that is not equally divisible by 6. No special characters are used in the final encoded string.
Let’s take that string we encoded to 6-bit chunks in binary and convert its values to decimal.
Binary: 010010 | 000110| 010101 | 101100
Decimal: 18 6 21 44
Now we simply match it’s corresponding value in decimal to the character in the Base64 table. 18 in decimal is S, 6 in decimal is G, 21 in decimal is V, and finally 44 in decimal is s.
Binary: 010010 | 000110 | 010101 | 101100
Decimal: 18 6 21 44
Value: S G V s
Our final result is: SGVs
Padding Base64
What about padding? Padding is needed when the number of characters to be encoded does not come with a multiple of six bits, therefore zeros will be used to complete the last bit sequence.
IMPORTANT NOTE: The first 12 bits (going from left to right) will get converted no matter what. If the second set of 6 bits are all zero’s , that still gets converted.
Padding with TWO equal signs.
Let’s convert the single lowercase letter of a.
a is 97 in decimal and 01100001 in binary. We end up with only 8 bits, which is not evenly divisible by six.
011000 | 01
Let’s fill up the remaining 16 bits with zeros then convert the values to decimal then look up the values in the Base64 table.
Binary: 011000 | 010000 | 000000 | 000000
Decimal: 24 16 [0] [0]
Value: Y Q
Since we had to add zero’s, those fake zeros get converted to an equal sign (=).
Binary: 011000 | 010000 | 000000 | 000000
Decimal: 24 16 [0] [0]
Value: Y Q = =
Our final result is: YQ==
Let’s convert H really quick. H is 72 in decimal or 01001000 in binary. Separate that into 6 bits, then add the remaining zeros.
010010 | 000000 | 000000 | 000000
Remember I said that the first 16 bits get converted no matter what? Well, our final result will be:
Binary: 010010 | 000000 | 000000 | 000000
Decimal: 18 0 [0] [0]
Value: S A = =
Our final result is: SA==
Padding with ONE equal sign.
Let’s convert the letters He. H is 72 in decimal or 01001000 in binary. e is 101 in decimal or 01100101 in binary. Let’s put those two (16 bits) together and pad 8 more bits at the end to end up with 24 bits. Then we split up everything into 6-bit chunks.
Decimal: 72 101
Binary: 01001000 01100101
0100100001100101 <- 00000000
Result: 010010 | 000110 | 010100 | 000000
Now we find the Decimal value for those 6-bit chunks then look up the value on the Base64 table. Since the last set of zeros were added or padded on, we can replace that with an equals sign (=).
Binary: 010010 | 000110 | 010100 | 000000
Decimal: 18 6 20 [0]
Value: S G U =
Our final result is: SGU=
Converting Hello World
Converting strings longer than 3 bytes (24 bits) holds the same process. Just convert every 3 bytes until you reach the end.
Let’s convert Hello World.
The first 3: Hel is SGVs. We have already converted this above. Here is the recap:
String: H e l
Decimal: 72 101 108
Binary: 01001000 | 01100101 | 01101100
------------------------------------------
Binary: 010010 | 000110 | 010101 | 101100
Decimal: 18 6 21 44
Value: S G V s
The next 3: lo . Note: There is a space after the lowercase o. Space is a special character but it still has a value on the ASCII table. It’s the 33rd item on that table, with a Decimal value of 32 and a hex value of 20.
String: l o [space]
Decimal: 108 111 32
Binary: 01101100 | 01101111 | 00100000
------------------------------------------
Binary: 011011 | 000110 | 111100 | 100000
Decimal: 27 6 60 32
Value: b G 8 g
The next 3: Wor
String: W o r
Decimal: 87 111 114
Binary: 01010111 | 01101111 | 01110010
------------------------------------------
Binary: 010101 | 110110 | 111101 | 110010
Decimal: 21 54 61 50
Value: V 2 9 y
The last two chars: ld. We will need padding for this.
String: l d
Decimal: 108 100
Binary: 01101100 | 01100100
------------------------------------------
Binary: 011011 | 000110 | 010000 | 000000
Decimal: 27 6 16 [0]
Value: b G Q =
Our final result is: SGVsbG8gV29ybGQ=
Other Base64 Implementations
Base64 in URLs and Filenames uses the Dash (-) and the Underscore (_) in the place of Plus Sign (+) and Forward Slash (/) and skips padding the encoded string with the Equals Sign (=). This is because URLs require special characters like + / = to be URL encoded into %2B, %2F and %3D respectively, and that makes the encoded result very long. This is part of the RFC4648 Spec which refers back to the RFC3548 Spec.
Continue to Part 2.